Density Estimators

Real-space on a rectangular grid

The simplest way to collect the density is to create a rectangular array of bins and histogram the beads of the paths. For example, a grid defined by

• xmin, xmax, nx
• ymin, ymax, ny
• zmin, zmax, nz

has nx*ny*nz rectangular bins, each with dimension dx = (xmax-xmin)/nx by dy = (ymax-ymin)/nz by dz = (zmax-zmin)/nz. The bin with indicies (i, j, k) is centered at ( xmin+(i+0.5)*dx, ymin+(j+0.5)*dy, zmin+(k+0.5)*dz ).

Each time a measurement is made, the position of all npart*nslice beads is checked, where npart is the number of particles of the species whose density is being measured. If a bead is inside one of the bins, that bin is increased by 1./nslice. If all beads lie in the grid bins, then the bins sum to npart. Otherwise the total is less than npart; this can happen if the grid dimensions do not fill the simulation supercell. To convert the measurement to density, divide by the volume of a bin, dx * dy * dz.

Sample pimc.xml code

<DensityEstimator>
  <Cartesian dir="x" nbin="500" min="-250 nm" max="250 nm"/>
  <Cartesian dir="y" nbin="500" min="-255 nm" max="250 nm"/>
</DensityEstimator>

Real-space on arbitrary grids

Density in k-space

Since pi-qmc uses a position basis, we often collect density fluctuations in real space. However, most textbook descriptions of density fluctioans are in k-space, and results for homogeneous systems are often best represented in k-space. Here we give a brief summary of common definitions for pedagogical purposes. For simplicity we write all formulas for spinless particles.

The dimensionsless Fourier transform of the density operator is (Eqs. 1.11 and 1.66 of Giuliani and Vignale)

(1)

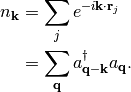
Note that 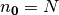, the total number of particles.

The pi code does not presently calculate this expectation value. If it is implemented in the future, it should return a complex expectation value for each k-vector. The imaginary part of this estimator will be zero for systems with inversion symmetry about the origin.

Homegeneous systems, such as liquid helium or the electron gas, will have 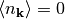for all 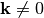. In those cases, it is better to calculate the static structure factor (see static structure factor).