Estimators: Describing the Measurements¶

List of All Estimators¶

AngularMomentumEstimator (scalar/angular-momentum) Measure the momentum in two-dimensions in a magnetic field.
BondLengthEstimator (scalar-length/bond-length) Measure the length of a molecular bond.
BoxEstimator (scalar/in-box) Measure the fraction of time a particle is in a boxed range.
CounductanceEstimator (dynamic-array/conductance) Measure dynamic correlations of current for polarizability.
CounductivityEstimator (dynamic-array/conductivity) Measure dynamic correlations of current density for conductivty.
CounductivityEstimator2D (dynamic-array/conductivity-2D) Measure dynamic correlations of current density for conductivty in two dimensions.
CoulombEnergyEstimator (scalar-energy/coulomb-energy) Measure the Coulomb energy using the thermodynamic estimator.
CountCountEstimator (dynamic-array/count-count) Measure the dynamic correlation of occupations on a grid.
DensCountEstimator (dynamic-array/density-count) Measure the dynamic correlation of density with occupations on a grid. (Not implemented.)
DensDensEstimator (dynamic-array/density-density) Measure dynamic correlations of density.
DensityEstimator (array/density) Measure particle density.
DiamagneticEstimator (scalar/diamagnetism) Measure diamagnetic susceptibility using path area.
DipoleEstimator (scalar-length/dipole) Measure the electric dipole of a localized, non-period system.
DynamicPCFEstimator (dynamic-array/pair-correlation) Measure the dynamic correlations of a pair correlation function.
EIndEstimator (dynamic-array/induced-e-field) Measure the induced electric field correction for the ConductivityEstimator.
EMARateEstimator (scalar/ema-recomination-rate) Measure electron and hole recombination rate.
FreeEnergyEstimator (histogram/free-energy) Measure relative free energies for different actions.
FrequencyEstimator (dynamic-scalar/frequency) Measure relative free energies for different actions.
JEstimator (array/singlet-triplet) Measure singlet-triplet splitting with mangetic field dependence.
PairCFEstimator (array/pair-correlation) Measure pair correlation functions.
PermutationEstimator (histogram/permutation) Measure distribution of permutations.
PositionEstimator (scalar-length/position) Measure average position of a particle.
SpinChargeEstimator (dynamic-array/spin-charge) Measure dynamic correlation of currents for different species.
ThermoEnergyEstimator (scalar-energy/thermo-energy) Measure the total energy using the thermodynamic estimator.
VIndEstimator (dynamic-scalar/induced-voltage) Measure the induced voltage correction for the ConductivityEstimator.
VirialEnergyEstimator (scalar-energy/virial-energy) Measure the total energy using the virial estimator.
WindingEstimator (histogram/winding) Measure distribution of periodic windings.
ZeroVarDensityEstimator (array/zero-var-density) Measure point-contact density with zero-varience within pair approximation.

Density Estimators¶

Real-space on a rectangular grid¶

The simplest way to collect the density is to create a rectangular array of bins and histogram the beads of the paths. For example, a grid defined by

xmin, xmax, nx
ymin, ymax, ny
zmin, zmax, nz

has nx*ny*nz rectangular bins, each with dimension dx = (xmax-xmin)/nx by dy = (ymax-ymin)/nz by dz = (zmax-zmin)/nz. The bin with indicies (i, j, k) is centered at ( xmin+(i+0.5)*dx, ymin+(j+0.5)*dy, zmin+(k+0.5)*dz ).

Each time a measurement is made, the position of all npart*nslice beads is checked, where npart is the number of particles of the species whose density is being measured. If a bead is inside one of the bins, that bin is increased by 1./nslice. If all beads lie in the grid bins, then the bins sum to npart. Otherwise the total is less than npart; this can happen if the grid dimensions do not fill the simulation supercell. To convert the measurement to density, divide by the volume of a bin, dx * dy * dz.

Sample pimc.xml code¶

<DensityEstimator>
  <Cartesian dir="x" nbin="500" min="-250 nm" max="250 nm"/>
  <Cartesian dir="y" nbin="500" min="-255 nm" max="250 nm"/>
</DensityEstimator>

Real-space on arbitrary grids¶

Density in k-space¶

Since pi-qmc uses a position basis, we often collect density fluctuations in real space. However, most textbook descriptions of density fluctioans are in k-space, and results for homogeneous systems are often best represented in k-space. Here we give a brief summary of common definitions for pedagogical purposes. For simplicity we write all formulas for spinless particles.

The dimensionsless Fourier transform of the density operator is (Eqs. 1.11 and 1.66 of Giuliani and Vignale)

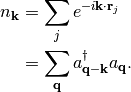
(1) $n_{\mathbf{k}} &= \sum_j e^{-i\mathbf{k}\cdot\mathbf{r}_j} \\ &= \sum_{\mathbf{q}} a^\dagger_\mathbf{q-k} a_{\mathbf{q}}.$

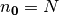Note that $n_{\boldsymbol{0}} = N$ , the total number of particles.

The pi code does not presently calculate this expectation value. If it is implemented in the future, it should return a complex expectation value for each k-vector. The imaginary part of this estimator will be zero for systems with inversion symmetry about the origin.

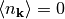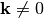Homegeneous systems, such as liquid helium or the electron gas, will have $\langle n_{\mathbf{k}}\rangle = 0$ for all $\mathbf{k} \ne 0$ . In those cases, it is better to calculate the static structure factor (see static structure factor).

Dynamic Response Functions¶

We define a dynamic correlation function as

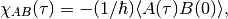
(2) $\chi_{AB}(\tau) = -(1/\hbar)\langle A(\tau)B(0)\rangle,$

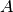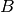where $A$ and $B$ are operators.

Density-density response¶

Since pi-qmc uses a position basis, we often collect density fluctuations in real space. However, most textbook descriptions of density fluctioans are in k-space, and results for homogeneous systems are often best represented in k-space. Here we give a brief summary of common definitions for pedagogical purposes. For simplicity we write all formulas for spinless particles.

The dimensionsless Fourier transform of the density operator is (Eqs. 1.11 and 1.66 of Giuliani and Vignale)

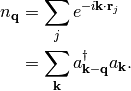
(3) $n_{\mathbf q} &= \sum_j e^{-i\mathbf{k}\cdot\mathbf{r}_j} \\ &= \sum_{\mathbf{k}} a^\dagger_{\mathbf{k}-\mathbf{q}}a_{\mathbf{k}}.$

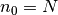Note that $n_0=N$ , the total number of particles. To get back to real-space density use

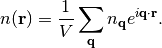
(4) $n(\mathbf{r}) = \frac{1}{V} \sum_{\mathbf{q}} n_{\mathbf{q}} e^{i\mathbf{q}\cdot\mathbf{r}}.$

For each of these, we define frequency-dependent density operators,

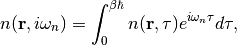
(5) $n(\mathbf{r},i\omega_n) = \int_0^{\beta\hbar} n(\mathbf{r},\tau) e^{i\omega_n\tau} d\tau,$

and

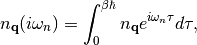
(6) $n_{\mathbf{q}}(i\omega_n) = \int_0^{\beta\hbar} n_{\mathbf{q}} e^{i\omega_n\tau} d\tau,$

where $i\omega_n = 2\pi ink_BT/\hbar$ are the Matsubara frequencies. Within the pi-qmc code, these frequency-dependent densities are easily calculated with fast Fourier transforms, which are most efficient when the number of slices is a power of two.

Real-space response¶

The imaginary-frequency response of the density to an external perturbation is given by (Ch 3.3 of Guiliani and Vignale),

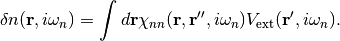
(7) $\delta n(\mathbf{r},i\omega_n) = \int d\mathbf{r} \chi_{nn}(\mathbf{r},\mathbf{r}'', i\omega_n) V_{\text{ext}}(\mathbf{r}', i\omega_n).$

In k-space this takes the convienent form,

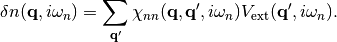
(8) $\delta n(\mathbf{q}, i\omega_n) = \sum_{\mathbf{q}'} \chi_{nn}(\mathbf{q}, \mathbf{q}', i\omega_n) V_{\text{ext}}(\mathbf{q}',i\omega_n).$

where the external potential in k-space satisfies

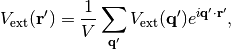
(9) $V_{\text{ext}}(\mathbf{r}') = \frac{1}{V} \sum_{\mathbf{q}'} V_{\text{ext}}(\mathbf{q}') e^{i\mathbf{q}'\cdot\mathbf{r}'},$

and

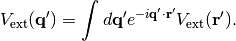
(10) $V_{\text{ext}}(\mathbf{q}') = \int d\mathbf{q}' e^{-i\mathbf{q}'\cdot\mathbf{r}'} V_{\text{ext}}(\mathbf{r}').$

These response functions are related to imaginary-frequency dynamic correlation functions,

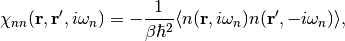
(11) $\chi_{nn}(\mathbf{r}, \mathbf{r}', i\omega_n) = -\frac{1}{\beta\hbar^2} \langle n(\mathbf{r} ,i\omega_n) n(\mathbf{r}',-i\omega_n)\rangle,$

and

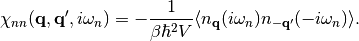
(12) $\chi_{nn}(\mathbf{q}, \mathbf{q}', i\omega_n) = -\frac{1}{\beta\hbar^2 V} \langle n_{\mathbf{q}}(i\omega_n) n_{-\mathbf{q}'}(-i\omega_n)\rangle.$

For a homogeneous system,

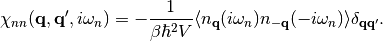
(13) $\chi_{nn}(\mathbf{q}, \mathbf{q}',i\omega_n) = -\frac{1}{\beta\hbar^2 V} \langle n_{\mathbf{q}}(i\omega_n) n_{-\mathbf{q}}(-i\omega_n)\rangle \delta_{\mathbf{q}\mathbf{q}'}.$

Structure factor¶

The dynamic structure factor S(k,iωn) measures the density response of the system,

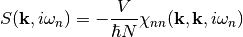
(14) $S(\mathbf{k}, i\omega_n) = -\frac{V}{\hbar N} \chi_{nn}(\mathbf{k}, \mathbf{k}, i\omega_n)$

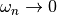The static structure factor is defined for equal time, not for $\omega_n \rightarrow 0$ ,

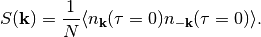
(15) $S(\mathbf{k}) = \frac{1}{N} \langle n_{\mathbf{k}}(\tau=0) n_{-\mathbf{k}}(\tau=0)\rangle.$

In terms of 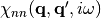$\chi_{nn}(\mathbf{q}, \mathbf{q}', i\omega)$ , the static structure factor is given by (prefactor is wrong)

(16) $S(\mathbf{k}) = -\frac{V}{\hbar N} \sum_n \omega_n \chi_{nn}(\mathbf{k}, \mathbf{k}, i\omega_n) e^{-i\omega_n\tau}.$

Table Of Contents

Previous topic

Next topic

This Page

Estimators: Describing the Measurements¶

List of All Estimators¶

Density Estimators¶

Real-space on a rectangular grid¶

Sample pimc.xml code¶

Real-space on arbitrary grids¶

Density in k-space¶

Dynamic Response Functions¶

Density-density response¶

Real-space response¶

Structure factor¶

Polarizability¶

Navigation

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Estimators: Describing the Measurements¶

List of All Estimators¶

Density Estimators¶

Real-space on a rectangular grid¶

Sample pimc.xml code¶

Real-space on arbitrary grids¶

Density in k-space¶

Dynamic Response Functions¶

Density-density response¶

Real-space response¶

Structure factor¶

Polarizability¶

Navigation